Oriented coloring

In graph theory, oriented graph coloring is a special type of graph coloring. Namely, it is an assignment of "colors" to vertices of an oriented graph that

is proper: no two adjacent vertices get the same color, and
respects the orientation: if (x, y) and (u, v) are arcs of the graph then it is not possible that colors of x and v and of y and u are the same.

An oriented chromatic number of a graph G is the least number of colors needed in an oriented coloring; it is usually denoted by 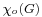$\scriptstyle\chi_o(G)$ .

Properties

We need an oriented graph, otherwise no oriented coloring exists. If the graph has loops (directed 2-cycles), the first (second, respectively) condition will be violated.

An oriented graph coloring corresponds to graph homomorphism into a tournament.

Examples

The oriented chromatic number of a directed 5-cycle is 5.